গ্রাফ থিওরি-৩ঃ ব্রেডথ ফার্স্ট সার্চের ব্যাবচ্ছেদ

ওকে । আমরা গ্রাফ তৈরী করলাম, গ্রাফ ইনপুটও নিয়ে ফেললাম। খুব ভালো কথা। কিন্তু এটা দিয়ে করবোটা কি? কি করবো সেই ব্যপারটা সবার আগে নির্ধারন করে নিতে হবে। আমরা চাই ০ নাম্বার নোড থেকে বাকি সব নোডের দুরত্ব বের করবো। কিন্তু কোন দুরত্ব? দুরত্ব নির্ভর করে আমরা কোন  পথ দিয়ে যাচ্ছি তার উপর।

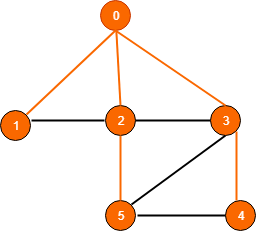
গ্রাফটা যেহেতু আনওয়েটেড সেহেতু সবগুলো এজ এর কস্ট সমান; ধরে নেই তা ১ ।  মানে হলো, ০ থেকে ১ এ যেতে যা, ০ থেকে ২ এ যেতে তা একইভাবে ২ থেকে ৩ এ যেতেও একই খরছ। এখন আমি যদি তোমাকে জিজ্ঞেস করি ০ থেকে ২ নাম্বার নোডে যেতে খরছ কত হবে? এখন খরছ কত হবে এটা নির্ভর করবে আমি কোন পথ দিয়ে যাচ্ছি। খেয়াল করো ০ থেকে ২ নাম্বার নোডে আসতে কিন্তু অনেকগুলো পথ আছে। আমরা পথ ও তাদের খরছের ছোটখাটো একটা হিসেব করে ফেলি-

পথ-১ঃ 0->1->2: 1+1 = 2
পথ-২ঃ 0->2: 1
পথ-৩ঃ 0->3->2: 2
পথ-৪ঃ 0->3->5->2: 1+1+1 = 3
পথ-৫ঃ 0->3->4->5->2: 1+1+1+1 = 4

দেখতেই পারছো শুধুমাত্র ২ তে আসার মোট পথ ৫ টা। আমরা সবচেয়ে ছোট পথটাই খুঁজে বের করবো। উপরের গ্রাফের ক্ষেত্রে ০->৩->২ বা কস্ট ২। আমরা সোর্স নোড থেকে প্রতিটা নোডের মিনিমাম কস্ট খুঁজে বের করবো।

শর্টেস্ট ডিস্টেন্ড বের করার অনেকগুলো অ্যালগরিদম আছে। তার মধ্যে একটা অ্যালগরিদম হল ব্রেডথ ফার্স্ট সার্চ। এই অ্যালগরিদম শুধুমাত্র আনওয়েটেড গ্রাফের ক্ষেত্রে কাজ করে। হোপফুলি ব্রেডথ ফার্স সার্চের কেন দরকার সে ব্যপারটা মোটামুটি ক্লিয়ার।

আমরা এখন দেখবো বিএফএস কিভাবে এই কাজটা করে-

প্রতিটা নোড থেকে তার এডজেসেন্ট নোডে ভিজিট করবো, কোন নোডে একবারের বেশী ভিজিট করা যাবেনা। 

০ যেহেতু আমাদের সোর্স নোড তাই এখান থকেই ট্রাভার্স শুরু করবো। তাইলে শুরু করে দেই-

• ০ তে ভিজিট করলাম। এই মুহুর্তে গ্রাফের অবস্থা। সোর্স নোডের দুরত্ব- ০

• ০ থেকে ১, ২, ৩ এ চলে গেলাম। সোর্স থেকে এদের দুরত্ব ০+১ = ১।  এই মুহুর্তে গ্রাফের অবস্থা- 

• ১ থেকে ২ এ পথ আছে কিন্তু ২ অলরেডি ভিজিটেড। ২ থেকে ৩ এ পথ আছে কিন্তু ৩ অলরেডি ভিজিটেড। আমরা ২ থেকে ৫ এ চলে গেলাম। এরপর ৩ থেকে শুধুমাত্র ৪ এ যেতে পারবো। সোর্স থেকে ৫ এবং ৪ এর দুরত্ব- ১+১ = ২।  এই মুহুর্তে গ্রাফের অবস্থা- 

যে পথগুলো আমরা ভিজিট করিনাই সেই পথগুলো বাদ দিলে পুরো গ্রাফটা একটা ট্রি হয়ে যায়। এর মানে হলো কোন নোডেই যাওয়ার জন্য একটার বেশী পথ পাবেনা। যে পথ আছে সেটাই সোর্স নোড থেকে  সর্বনিন্ম পথ। আমি আনইউজড পথগুলো হাল্কা করে দিচ্ছি। খেয়াল করলেই বুঝতে পারবা-

এই কাজটা কোডে রূপান্তর করা একদমই সোজা। আমরা প্রতিটা নোড থেকে তার সংগলগ্ন নোডগুলোতে যাওয়ার চেষ্টা করবো। যদি যেতে পারি তাহলে সেই নোডটাকে ভিজিটেড মার্ক করে দিবো। কিন্তু কোন নোডের পর কোন নোডে কাজ করবো সেই সিকুয়েন্স মেন্টেন করার জন্য কিউ ডেটা স্ট্রাকচার ব্যবহার করবো। অথ্যাৎ, কিউ থেকে একটা একটা করে নোড নিয়ে আসবো এবং সে নোডের অ্যাডজেসেন্ট নোডগুলোতে ভিজিট করবো। ভিজিট করা নোডগুলোকে কিউ তে পুশ করবো। এই কাজটা করতে থাকবো কিউ খালি হওয়া পর্যন্ত। পুরো ব্যাপারটা আসলে এমন-

১। সোর্স নোডকে ভিজিটেড মার্ক করা এবং  কিউ তে পুশ করা
২। কিউ থেকে পপ করা
৩। পপ করা নোডের এডজেসেন্ট নোডগুলোতে ভিজিটেড মার্ক করা এবং সেগুলোকে কিউতে পুশ করা।
৪। ২, ৩ চলতে থাকবে যতক্ষণ না কিউ খালি হয়

সুডোকোডঃ

 create a queue Q   
 mark v as visited and put v into Q   
 while Q is non-empty   
   remove the head u of Q   
   mark all the neighbours as visited and enqueue all (unvisited) neighbours of u  

যেহেতু আমাদেরকাজ হলো সোর্স থেকে প্রতিটা নোডের ডিস্টেন্স বের করা সেহেতু কোন নোড ভিজিটেড হয়ে গেলে তার ডিস্টেন্সটা distance[] নামক একটা অ্যারেতে রাখবো।  সোর্সের ডিস্টেন্স যেহেতু ০ তাই distance[source] = 0 হবে। এভাবে বাকিগুলো।

পুরো ঘটনাকে যদি সিমুলেট করি -

স্টেপ- ১ঃ ০ তে ভিজিট করলাম। একে কিউ তে পুশ করি। distance[0] = 0

Queue- 0

স্টেপ- ২ঃ কিউ থেকে একটা আইটেম পপ করলে পাবো নোড ০ কে। ০ থেকে যাওয়া যায় ১, ২, ৩ এ। এই তিনটাকে ভিজিটেড হিসেবে মার্ক করি।
distance[1] = distance[0]+1, distance[2] = distance[0]+1, distance[3] = distance[0]+1
১, ২, ৩ কে কিউতে পুশ করি-

Queue: 1 2 3

স্টেপ- ৩ঃ কিউ কে পপ করলে ১ পাবো। ১ থেকে যাওয়া যায় ২ তে। কিন্তু ২ অলরেডি ভিজিটেড। তাই কিছুই করবোনা।

Queue: 2 3

স্টেপ- ৪ঃ কিউ থেকে আবার পপ করলে পাবো ২ । ২ থেকে ৩ ও ৫ যাওয়া যায়। কিন্তু ৩ যেহেতু অলরেডি ভিজিটেড আমরা শুধু ৫ এ ভিজিট করবো। distance[5] = distance[2]+1. ৫ কে কিউতে পাঠিয়ে দেই

Queue: 3 5

স্টেপ- ৫ঃ এবার পপ করলে ৩ কে পাবো । ৩ থেকে ৫ ও ৪ এ যাওয়া যায়। ৫ অলরেডি ভিজিটেড। আমরা শুধু ৪ এ যাবো। distance[4] = distance[3]+1.  ৪ কে কিউ তে পুশ করি

Queue: 5 4

স্টেপ- ৬ঃ আবার পপ করলে পাবো ৫ কে। ৫ এর এডজেসেন্ট নোড সব ভিজিটেড। তাই কিছু করবোনা।

Queue: 4 

স্টেপ- ৭ঃ ৪ কে পপ করি। ৪ থেকেও কোথাও যাওয়া যায়না।

Queue: 

স্টেপ- ৮ঃ কিউ ফাঁকা। কাজ শেষ। খেয়াল করো, আমরা কিন্তু distance অ্যারের ভিতর সবগুলো নোডের দুরত্ব পেয়ে গেছি।

বুঝতেই পারছো কোডে ইমপ্লিমেন্ট করার সময় একটা কিউ ডেটা স্ট্রাকচার লাগবে। তুমি চাইলে লাইব্রেরি ইউজ করতে পারো অথবা নিজেই বানাতে পারো। পুরো কোডটা প্রথমে নিজে ইমপ্লিমেন্ট করার চেষ্টা করো। তারপর নীচের কোডটা দেখো-

 while(!q.empty())  
   {  
     int u = q.front();  
     q.pop();  
     printf("%d ", u);  
     for(v = 0; v<g[u].size(); v++)  
     {  
       int adjecentNodeofU = g[u][v];  
       if(visited[adjecentNodeofU] == 0)  
       {  
         visited[adjecentNodeofU] = 1;  
         level[adjecentNodeofU] = level[u]+1;  
         q.push(adjecentNodeofU);  
       }  
     }  
     cout<<endl;  
   }  

পুরো কোড পাওয়া যাবে এখানেঃ
১। BFS using Adjacency Matrix
২। BFS using Adjacency List