ডাটা স্ট্রাকচার - ১১ঃ হিপসর্ট

হিপ পদ্ধতি অবলম্বন করে যে ধরনের সর্ট করা হয় তাকেই হিপ সর্ট বলে। আমরা জানি হিপে রুট নোডটা থাকে সবচেয়ে বড়। হিপ সর্টে সেই রুট নোডটাকে সবার শেষের নোডের সাথে সোয়াপ করা হয়। তারপর শেষের নোডটা বাদ দিয়ে পুরো ট্রি টাকে আবার হিপে রুপান্তর করা হয়। এভাবে সোয়াপ এবং হিপে রুপান্তরের এক পর্যায়ে পুরো ট্রি টা সর্ট হয়ে যায়। নীচের সিমুলেশনটা খেয়াল করো-

সোয়াপ করার পর প্রতিবার আমরা শেষ থেকে একটা করে নোড বাদ দিয়ে বাকি অংশটাকে হিপিফাই করতেছি। এভাবে একটা পর্যায়ে গিয়ে পুরো ট্রি টাই সর্ট হয়ে যায়। কোডে রুপান্তর আরো সোজা-

 void heapSort(int heap[], int heapSize)  
 {  
   int i, temp;  
   buildMaxHeap(heap, heapSize); //Building heap  
   for(i = heapSize; i>1; i--)  
   {  
     temp = heap[1];  
     heap[1] = heap[heapSize];  
     heap[heapSize] = temp;  
     heapSize--;  
     maxHefipy(heap, heapSize, 1);  
   }  
 }  

ডাটা স্ট্রাকচার - ১০ঃ হিপ

হিপঃ হিপ হলো একটি কমপ্লিট বাইনারি ট্রি যে ট্রি এর প্রতিটি নোড তার চাইল্ড নোডের চেয়ে বড় বা ছোট থাকে থাকে। যদি বড় থাকে তাকে ম্যাক্স হিপ বলে আর যদি ছোট থাকে তাকে মিন হিপ বলে। এখানে আমরা শুধু ম্যাক্স হিপ নিয়েই ত্যানা পেঁচাবো। উপরে একটি ফিগার দেওয়া হলো-

একটি ট্রি কে অ্যারেতে স্টোর করার একমাত্র অসুবিধা হল কার চাইল্ড কে হবে তা আইডেন্টিফাই করতে না পারা। হিপ যেহেতু একটা কমপ্লিট বাইনারি ট্রি সে সুবিধা প্রয়োগ করে আমরা হিপকে একটা অ্যারেতে স্টোর করতে পারি এবং খুব সুন্দরভাবেই কোন ইন্ডেক্সের চাইল্ড কে তা বের করে আনতে পারি। উপরের ট্রি কেই অ্যারে আকারে লিখলাম ০ নাম্বার ইন্ডেক্স বাদ দিয়ে। খেয়াল করো।

এখন কোন ইন্ডেক্সের চাইল্ড কে হবে সেটি বের করতে পারলেই আমাদের সমস্যা শেষ। নীচের স্টেটমেন্টগুলো লক্ষ্য করো এবং অ্যারের ইন্ডেক্সগুলোর সাথে মিলিয়ে দেখো-

heap[0] = 0
heap[1] = 90
heap[2] = 85
heap[3] = 80
heap[2*2] = 70 // Left Child of 2
heap[2*2+1] = 60 //Right Child of 2
heap[3*3] = 55 //Left child of 3
heap[3*3+1] = 50 //Right Child of 3

সো, এখান থেকে এই জিনিসট স্পষ্ট যে কোন একটি ইন্ডেক্স যদি হয় i তাহলে তার লেফট চাইল্ড এর ইন্ডেক্স হবে i*i এবং রাইট চাইল্ড এর ইন্ডেক্স হবে i*i+1 । আবার তার প্যারেন্ট কে তার জন্য i কে দুই দিয়ে ইন্টেজার ডিভিশন করলেই কাজ শেষ । সো, এই কথাগুলোকেই কোডে আকারে লিখে ফেলি-

 int left(int i)  
 {  
   return 2*i;  
 }  
 int right(int i)  
 {  
   return (2*i)+1;  
 }  
 int parent(int i)  
 {  
   return i/2;  
 }  

নির্দিষ্ট কিছু ডেটাকে হিপ আকারে রাখার অ্যালগরিদমঃ

1. Find the left child and right child particular index
2. Find the biggest index between left, right and the particular index. Then swap the value of the biggest index and the particular index.
3. Do it until the biggest index is found in the left or right child

Pseudo Code:

 void maxHefipy(int heap[], int heapSize, int i)  
 {  
   int l, r, largest;  
   l = left(i);  
   r = right(i);  
   if(l<=heapSize && heap[l]>heap[i])  
   {  
     largest = l;  
   }  
   else  
   {  
     largest = i;  
   }  
   if(r<=heapSize && heap[r]>heap[largest])  
   {  
     largest = r;  
   }  
   if(largest!= i)  
   {  
     int temp = heap[i];  
     heap[i] = heap[largest];  
     heap[largest] = temp;  
     maxHefipy(heap, heapSize, largest);  // maxHefipy again from the largest index
   }  
 }  

একটি নোডের সবগুলো সাবট্রি যদি হিপ হয় সেক্ষেত্রে ওই নোডকে একবার কল করলেই এই অ্যালগরিদম দিয়ে পুরোপুরি হিপিফাই করা যাবে। উপরের চিত্রটি ভালোভাবে খেয়াল করলে বুঝতে পারবে।

কিন্তু ট্রি তে ডেটা যদি অন্যভাবে সাজানো থাকে তাহলে কিন্তু উপরের মত কাজ করবেনা। নীচের চিত্রে খেয়াল করো একবার কল করার পরই রিকার্সিভ কল বন্ধ হয়ে যাচ্ছে। কারন ৪ দিয়ে আর কল করা যাচ্ছেনা।

এই পরিস্থিতিতে maxHeapify() কে একাধিকবার কল করতে হবে। উপরের অ্যালগরিদমটাই N/2 বার কল করলেই পুরো ট্রি টা ১০০% হিপিফাই হয়ে যাবে। হিপিফাই করবো N/2 তম ইন্ডেক্স থেকে শূরু করে প্রথম ইন্ডেক্স পর্যন্ত। উপরের ট্রি এর ক্ষেত্রে এটা হবে 5/2 = 2 (ইন্টেজার ডিভিশন)। তো বুঝতেই পারছো এখানে আমাদের লুপ ব্যাবহার করতে হবে।

 void createMaxHeap(int heap[], int heapSize)  
 {  
   int i;  
   for(i = heapSize/2; i>=1; i--)  
   {  
     maxHefipy(heap, heapSize, i);  
   }  
 }  

নীচের সিমুলেশনটা খেয়াল করো-

কি! ক্লিয়ার না কোন ভেজাল আছে? ভেজাল থাকে কমেন্ট করে জানাইতে পারো। 

ডাটা স্ট্রাকচার - ৪ঃ ডবলি লিংক লিস্ট

এর আগে আমরা যে লিংক লিস্ট নিয়ে কাজ করেছি সেখানে শুধু একদিক থেকে যাওয়া যায়। দুই দিক থেকে যাওয়া যায়না। যেমন ধরো, আমি ১০ থেকে শুরু করে লিস্টের ৫০ পর্যন্ত গেলাম। আবার ৫০ থেক শুরু করে যদি ১০ পর্যন্ত আসতে চাই তাহলে সিংগ লিংক লিস্টে সেটা সম্ভব না।

অথ্যাৎ, দ্বিমুখী না। দ্বিমুখী না হওয়ার কারন একটাই কারন আমরা প্রতিটা নোডে শুধু নেক্সট নোডেরই অ্যাড্রেস রাখি, এর আগে যে থাকবে সে  অ্যাড্রেসটা ধরে রাখিনা। ডবলি লিংক লিস্ট এমন ধরনের লিংক লিস্ট যেখানে প্রতিটা নোড একইসাথে নেক্সট জনের অ্যাড্রেস ধরে রাখে এবং প্রিভিয়াস জনের অ্যাড্রেসও ধরে রাখে। চিত্রে প্রথমটা সিংগলি লিঙ্ক লিস্ট পরেরটি ডাবলি লিঙ্ক লিস্ট। ডবলি লিঙ্ক লিস্টে আমরা দুই দিক থেকেই আসা যাওয়া করতে পারবো। 

ইমপ্লিমেন্টেশনঃ ইমপ্লিমেন্টেশন আগের মতই শুধু নোড তৈরী করার সময় Previous নোড রাখার জন্য একটা এক্সট্রা পয়েন্টার রাখতে হবে একইভাবে ডেটা ইন্সার্ট করার সময় Next Node এর পাশাপাশি Previous Node কে  হবে তা নির্দিষ্ট করে দিতে হবে।  বাকি সব আগের মতই। আমরা লিংক লিস্টের কোডটাই মডিফাই করে ডবলি লিংক লিস্ট আকারে লিখতে পারি-

 void inserEnd(int value)  
 {  
   if(sefuda == NULL)  
   {  
     person = (node*)malloc(sizeof(node));  
     person->data = value;  
     person->prev = NULL;  
     person->next = NULL;  
     sefuda = person;  
     current = sefuda;  
   }  
   else  
   {  
     person->next = (node*)malloc(sizeof(node));  
     person = person->next;  
     person->data = value;  
     person->prev = current;  
     person->next = NULL;  
     current = person;  
   }  
 }  

ডাটা স্ট্রাকচার - ৬ঃ বাইনারি ট্রি ট্রাভার্সাল

এই পর্বে আমরা শিখবো কিভাবে একটা বাইনারি ট্রি এর মধ্যে ট্রাভার্স করতে হয়। একটা ডাটা স্ট্রাকচারের ডেটাগুলো অ্যাক্সেস করার ক্ষেত্রে ট্রাভার্সাল জিনিসটা অনেক বেশী গুরুত্বপুর্ন। বাইনারি ট্রিতে ৩ ভাবে ট্রাভার্সাল চালানো যায়-

১। প্রি অর্ডার(Pre Order): প্রথমে রুট, তারপর লেফট, তারপর রাইটে যেতে হয়- Root->Left->Right-
 2, 7, 1, 6, 5, 10, 9, 8, 3, 4

২। ইন অর্ডার(In Order):  প্রথমে লেফট, তারপর রুট তারপর রাইট- Left->Root->Right:
1, 7,  5, 6, 10, 2, 9, 3, 8, 4

৩। পোস্ট অর্ডার(Post Order): প্রথমে লেফট তারপর রাইট এবং সবশেষে রুট- Left->Right->Root :
1, 5, 10, 6, 7, 3, 4, 8, 9, 2


ব্যাপারটা কিন্তু একদম সহজ, ইনঅর্ডারের ক্ষেত্রে আমরা সিমুলেট করে দেখি- বোঝার সুবিদার্থে আমরা মার্কার নামক একটা শব্দ ব্যাবহার করবো। ভিবিন্ন নোডে মুভ করবে, যখন যেখানে থাকবে সেটাকে আমরা ওই সময়ে রুট হিসেবে চিন্তা করবো যদি সেই নোডের চাইল্ড থাকে। 

ট্রাভার্সালের একদম শুরুতে মার্কার থাকবে দুই নোড- ২ তে। তার মানে এই মুহুর্তে রুট হল ২। কিন্তু নিয়মুনাযায়ী প্রথমে নিতে হবে লেফট কে। তাই মার্কার এখন লেফট এ চলে যাবে তা হল ৭। ৭ এরদুটো চাইল্ড আছে তার মানে ৭ হল তাদের রুট।  আবার ৭ এর আবার লেফট চাইল্ড আছে,  তাই বামে মুভ করবো আর তা হল- ১। মার্কার এখন ১ এ আছে। ১ এর কোন চাইল্ড নাই তাই এটাকে আমরা নিয়ে নিবো। তারপর এই নোডের জন্য যে, রুট তাকে নিয়ে নিবো। আর সেটা হল ৭। ৭ এর লেফট এবং রুট নেওয়া হল। বাকি থাকলো রাইট। মার্কার এখন ৭ এ রাইট চাইল্ডে যাবো। কিন্তু রাইট চাইল্ডের আবার লেফট চাইল্ড আছে তা হল ৬।  মার্কার এখন ৬ এ আছে। কিন্তু ৬ এর যেহেতু লেফট চাইল্ড আছে আমরা লেফটে চলে যাবো। তার মানে আমাদের মার্কার এখন ৫ এ। লেফট নিলাম এখন ৫ এর রুট নিবো আর তা হলো ৬। রুট নিলাম এখন বাকি আছে রাইট তা হলো ১০ । খেয়াল করো ২ এর লেফট নেওয়া হয়ে গেছে। এখন রুট নিবো তা হলো ২। লেফট, রুট নেওয়া হয়ে গেছে এখন বাকি আছে রাইট।

মার্কার এখন ৯ এ আছে। ৯ এর যেহেতু কোন লেফট নাই তাই লেফট থেকে নেওয়ার কিছু নাই। লেফট গেলো এখন নিবো রুট আর তা হল ৯। বাকি আছে রাইট। ৯ এর রাইটে আছে ৮। আমাদের মার্কার এখন ৮ এ ।  ৮ এর লেফট চাইল্ড ৩। মার্কার এখন ৩ এ। ৩ এর যেহেতু কোন চাইল্ড নাই ৩ ই হল ৮ এর লেফট। লেফট গেলো এখন বাকি আছে রুট। রুট হল ৮ । এখন বাকি আছে রাইট মার্কার এখন ৪ এ! ৪ কে নেই।

এভাবে বাকিগুলো নিজে নিজে সিমুলেট করে দেখো।


ইমপ্লিমেন্টেশনঃ
রিকার্সন দিয়ে এই কাজটা খুব সহজেই করা যায়। কেউ চাইলে লুপ দিয়েও করতে পারে-

 void preOrder(Node *node)  
 {  
   printf("%d ", node->data);  //print root
   if(node->left!= NULL){  //if there is any left child go to left 
     preOrder(node->left);  
   }  
   if(node->right!= NULL){  //if there is any right child go to right 
     preOrder(node->right);  
   }  
 }  

 void inOrder(Node *node)  
 {  
   if(node->left!= NULL){  //if there is any left child go to left 
     inOrder(node->left);  
   }  
   printf("%d ", node->data);  //print the root 
   if(node->right!= NULL){  //if there is any right child go to right
     inOrder(node->right);  
   }  
 }  

 void postOrder(Node *node)  
 {  
   if(node->left!= NULL){  //if there is any left child go to left 
     postOrder(node->left);  
   }  
   if(node->right!= NULL){  //if there is any right child go to right 
     postOrder(node->right);  
   }  
   printf("%d ", node->data);  //print the root 
 }  

গ্রাফ থিওরি-৩ঃ ব্রেডথ ফার্স্ট সার্চের ব্যাবচ্ছেদ

ওকে । আমরা গ্রাফ তৈরী করলাম, গ্রাফ ইনপুটও নিয়ে ফেললাম। খুব ভালো কথা। কিন্তু এটা দিয়ে করবোটা কি? কি করবো সেই ব্যপারটা সবার আগে নির্ধারন করে নিতে হবে। আমরা চাই ০ নাম্বার নোড থেকে বাকি সব নোডের দুরত্ব বের করবো। কিন্তু কোন দুরত্ব? দুরত্ব নির্ভর করে আমরা কোন  পথ দিয়ে যাচ্ছি তার উপর।

গ্রাফটা যেহেতু আনওয়েটেড সেহেতু সবগুলো এজ এর কস্ট সমান; ধরে নেই তা ১ ।  মানে হলো, ০ থেকে ১ এ যেতে যা, ০ থেকে ২ এ যেতে তা একইভাবে ২ থেকে ৩ এ যেতেও একই খরছ। এখন আমি যদি তোমাকে জিজ্ঞেস করি ০ থেকে ২ নাম্বার নোডে যেতে খরছ কত হবে? এখন খরছ কত হবে এটা নির্ভর করবে আমি কোন পথ দিয়ে যাচ্ছি। খেয়াল করো ০ থেকে ২ নাম্বার নোডে আসতে কিন্তু অনেকগুলো পথ আছে। আমরা পথ ও তাদের খরছের ছোটখাটো একটা হিসেব করে ফেলি-

পথ-১ঃ 0->1->2: 1+1 = 2
পথ-২ঃ 0->2: 1
পথ-৩ঃ 0->3->2: 2
পথ-৪ঃ 0->3->5->2: 1+1+1 = 3
পথ-৫ঃ 0->3->4->5->2: 1+1+1+1 = 4

দেখতেই পারছো শুধুমাত্র ২ তে আসার মোট পথ ৫ টা। আমরা সবচেয়ে ছোট পথটাই খুঁজে বের করবো। উপরের গ্রাফের ক্ষেত্রে ০->৩->২ বা কস্ট ২। আমরা সোর্স নোড থেকে প্রতিটা নোডের মিনিমাম কস্ট খুঁজে বের করবো।

শর্টেস্ট ডিস্টেন্ড বের করার অনেকগুলো অ্যালগরিদম আছে। তার মধ্যে একটা অ্যালগরিদম হল ব্রেডথ ফার্স্ট সার্চ। এই অ্যালগরিদম শুধুমাত্র আনওয়েটেড গ্রাফের ক্ষেত্রে কাজ করে। হোপফুলি ব্রেডথ ফার্স সার্চের কেন দরকার সে ব্যপারটা মোটামুটি ক্লিয়ার।

আমরা এখন দেখবো বিএফএস কিভাবে এই কাজটা করে-

প্রতিটা নোড থেকে তার এডজেসেন্ট নোডে ভিজিট করবো, কোন নোডে একবারের বেশী ভিজিট করা যাবেনা। 

০ যেহেতু আমাদের সোর্স নোড তাই এখান থকেই ট্রাভার্স শুরু করবো। তাইলে শুরু করে দেই-

• ০ তে ভিজিট করলাম। এই মুহুর্তে গ্রাফের অবস্থা। সোর্স নোডের দুরত্ব- ০

• ০ থেকে ১, ২, ৩ এ চলে গেলাম। সোর্স থেকে এদের দুরত্ব ০+১ = ১।  এই মুহুর্তে গ্রাফের অবস্থা- 

• ১ থেকে ২ এ পথ আছে কিন্তু ২ অলরেডি ভিজিটেড। ২ থেকে ৩ এ পথ আছে কিন্তু ৩ অলরেডি ভিজিটেড। আমরা ২ থেকে ৫ এ চলে গেলাম। এরপর ৩ থেকে শুধুমাত্র ৪ এ যেতে পারবো। সোর্স থেকে ৫ এবং ৪ এর দুরত্ব- ১+১ = ২।  এই মুহুর্তে গ্রাফের অবস্থা- 

যে পথগুলো আমরা ভিজিট করিনাই সেই পথগুলো বাদ দিলে পুরো গ্রাফটা একটা ট্রি হয়ে যায়। এর মানে হলো কোন নোডেই যাওয়ার জন্য একটার বেশী পথ পাবেনা। যে পথ আছে সেটাই সোর্স নোড থেকে  সর্বনিন্ম পথ। আমি আনইউজড পথগুলো হাল্কা করে দিচ্ছি। খেয়াল করলেই বুঝতে পারবা-

এই কাজটা কোডে রূপান্তর করা একদমই সোজা। আমরা প্রতিটা নোড থেকে তার সংগলগ্ন নোডগুলোতে যাওয়ার চেষ্টা করবো। যদি যেতে পারি তাহলে সেই নোডটাকে ভিজিটেড মার্ক করে দিবো। কিন্তু কোন নোডের পর কোন নোডে কাজ করবো সেই সিকুয়েন্স মেন্টেন করার জন্য কিউ ডেটা স্ট্রাকচার ব্যবহার করবো। অথ্যাৎ, কিউ থেকে একটা একটা করে নোড নিয়ে আসবো এবং সে নোডের অ্যাডজেসেন্ট নোডগুলোতে ভিজিট করবো। ভিজিট করা নোডগুলোকে কিউ তে পুশ করবো। এই কাজটা করতে থাকবো কিউ খালি হওয়া পর্যন্ত। পুরো ব্যাপারটা আসলে এমন-

১। সোর্স নোডকে ভিজিটেড মার্ক করা এবং  কিউ তে পুশ করা
২। কিউ থেকে পপ করা
৩। পপ করা নোডের এডজেসেন্ট নোডগুলোতে ভিজিটেড মার্ক করা এবং সেগুলোকে কিউতে পুশ করা।
৪। ২, ৩ চলতে থাকবে যতক্ষণ না কিউ খালি হয়

সুডোকোডঃ

 create a queue Q   
 mark v as visited and put v into Q   
 while Q is non-empty   
   remove the head u of Q   
   mark all the neighbours as visited and enqueue all (unvisited) neighbours of u  

যেহেতু আমাদেরকাজ হলো সোর্স থেকে প্রতিটা নোডের ডিস্টেন্স বের করা সেহেতু কোন নোড ভিজিটেড হয়ে গেলে তার ডিস্টেন্সটা distance[] নামক একটা অ্যারেতে রাখবো।  সোর্সের ডিস্টেন্স যেহেতু ০ তাই distance[source] = 0 হবে। এভাবে বাকিগুলো।

পুরো ঘটনাকে যদি সিমুলেট করি -

স্টেপ- ১ঃ ০ তে ভিজিট করলাম। একে কিউ তে পুশ করি। distance[0] = 0

Queue- 0

স্টেপ- ২ঃ কিউ থেকে একটা আইটেম পপ করলে পাবো নোড ০ কে। ০ থেকে যাওয়া যায় ১, ২, ৩ এ। এই তিনটাকে ভিজিটেড হিসেবে মার্ক করি।
distance[1] = distance[0]+1, distance[2] = distance[0]+1, distance[3] = distance[0]+1
১, ২, ৩ কে কিউতে পুশ করি-

Queue: 1 2 3

স্টেপ- ৩ঃ কিউ কে পপ করলে ১ পাবো। ১ থেকে যাওয়া যায় ২ তে। কিন্তু ২ অলরেডি ভিজিটেড। তাই কিছুই করবোনা।

Queue: 2 3

স্টেপ- ৪ঃ কিউ থেকে আবার পপ করলে পাবো ২ । ২ থেকে ৩ ও ৫ যাওয়া যায়। কিন্তু ৩ যেহেতু অলরেডি ভিজিটেড আমরা শুধু ৫ এ ভিজিট করবো। distance[5] = distance[2]+1. ৫ কে কিউতে পাঠিয়ে দেই

Queue: 3 5

স্টেপ- ৫ঃ এবার পপ করলে ৩ কে পাবো । ৩ থেকে ৫ ও ৪ এ যাওয়া যায়। ৫ অলরেডি ভিজিটেড। আমরা শুধু ৪ এ যাবো। distance[4] = distance[3]+1.  ৪ কে কিউ তে পুশ করি

Queue: 5 4

স্টেপ- ৬ঃ আবার পপ করলে পাবো ৫ কে। ৫ এর এডজেসেন্ট নোড সব ভিজিটেড। তাই কিছু করবোনা।

Queue: 4 

স্টেপ- ৭ঃ ৪ কে পপ করি। ৪ থেকেও কোথাও যাওয়া যায়না।

Queue: 

স্টেপ- ৮ঃ কিউ ফাঁকা। কাজ শেষ। খেয়াল করো, আমরা কিন্তু distance অ্যারের ভিতর সবগুলো নোডের দুরত্ব পেয়ে গেছি।

বুঝতেই পারছো কোডে ইমপ্লিমেন্ট করার সময় একটা কিউ ডেটা স্ট্রাকচার লাগবে। তুমি চাইলে লাইব্রেরি ইউজ করতে পারো অথবা নিজেই বানাতে পারো। পুরো কোডটা প্রথমে নিজে ইমপ্লিমেন্ট করার চেষ্টা করো। তারপর নীচের কোডটা দেখো-

 while(!q.empty())  
   {  
     int u = q.front();  
     q.pop();  
     printf("%d ", u);  
     for(v = 0; v<g[u].size(); v++)  
     {  
       int adjecentNodeofU = g[u][v];  
       if(visited[adjecentNodeofU] == 0)  
       {  
         visited[adjecentNodeofU] = 1;  
         level[adjecentNodeofU] = level[u]+1;  
         q.push(adjecentNodeofU);  
       }  
     }  
     cout<<endl;  
   }  

পুরো কোড পাওয়া যাবে এখানেঃ
১। BFS using Adjacency Matrix
২। BFS using Adjacency List 

ওয়াইফাই থেকে ডেটা সেইভ রাখা আসলেই সম্ভব?

মোবাইল, ল্যাপটপ সহ সমস্ত ইলেক্ট্রিক ডিভাইস চার্জ করে পরবর্তীতে ব্যবহার করা যায়। এই জিনিসটাই আমাদের জীবন ব্যবস্থা কতটা সহজ করে ফেলছে তা কল্পনা করা যাবেনা। পাওয়ার ব্যাংক চার্জ করে মানুষ দুনিয়া ঘুরে। পাহাড় কিম্বা সাগরের মাঝখানে সব যায়গায় সচল থাকে ইলেক্ট্রিক ডিভাইস। ইলেক্ট্রিসিটি সংরক্ষণের এই পদ্ধতির আবিষ্কারককে সম্ভব হলে আমি নোবেল দিতাম। যাইহোক ইলেক্ট্রিক ডিভাইস নিয়ে কথা বলা আলোচ্য বিষয় না।

একজন সেলুলার নেটওয়ার্ক ইউজারের কাছে ওয়াইফাই কিম্বা ব্রডব্যান্ডের গুরুত্ব কতটা তা মোটামুটি সবাই জানি। যে জন্মের পর পরই ওয়াইফাই এর চেহারা দেখছে কিম্বা জীবনে কখনো মোবাইল ডেটা ব্যাবহার করার দরকার পড়েনাই তার কথা বাদই দিলাম; যদিও আমি মনে করিনা সেরকম প্রাণী বাংলাদেশে এখনো জন্ম নিয়েছে। আর যে প্রথম ওয়াইফাই এর চেহারা দেখছে তার কাছে এইটার অনুভূতি অনেকটা মানুষখোর বাঘের মত কিম্বা বিরিয়ানি খাদকের মত।  এখনো মনে পড়ে শুধু ওয়াইফাই এর জন্য বসুন্ধরায় গিয়ে কত কত সময় পার করছি।

যাইহোক, স্বাভাবিকভাবে প্রশ্ন আসবেই যদি এই ডেটা সংগ্রহ করে যদি বাসায় নিয়ে যাই তাহলে একই স্পিডে বিনা খরছে নেট ব্রাউজ করতে পারবো। এটা খুবই স্বাভাবিক এবং মজার একটা প্রশ্ন! এই প্রশ্নটা করার মানে হলো ইন্টারনেট কিভাবে কাজ করে এই ব্যপার সম্পর্কে তার আইডিয়া নাই। আমার তো ধারনা ৯০% ইন্টারনেট ইউজারই জানেনা আসলে এই জিনিসটা কিভাবে কাজ করে। কিন্তু আমাদের এমন একটা জাতি কেউ যখন সাহস করে কোন প্রশ্ন করে উত্তর নিজে জানি আর না জানি  পচাইতে পচাইতে রীতিমত প্রশ্নকর্তার প্যান্ট খুলে দেই। যাইহোক আমি নেটওয়ার্কিং এর ক্ষুদ্র জ্ঞানে  সবার কাছে সহজবোধ্য করে বুঝানোর চেষ্টা করবো আসলে ব্যাপারটা কি!

মনে করুন আপনার পিসির সাথে আপনার ফোন ডেটাকেবল দিয়ে কানেক্টেড। আপনি চাইলে আপনার পিসি দিয়ে ফোনের সব ডেটা দেখতে পাবেন। একইভাবে আপনার দুইটা পিসি যদি পরস্পর ক্যাবল দিয়ে কানেক্টেড হয় তাহলে এক পিসি থেকে অন্য পিসির সমস্ত ডেটা দেখতে পাবেন। ডেটা বলতে আমি বুঝাচ্ছি অডিও, ভিডিও, ছবি, অন্যন্য ডকুমেন্টস। আপনার একটা পিসি যদি উগান্ডা থাকে এবং একইভাবে ক্যাবল দিয়ে কানেক্টেড থাকে তাহলে আপনি চাইলে বাংলাদেশে বসেই ওই পিসিতে যা যা আছে সবই দেখতে পাবেন বা ট্রান্সফার করতে পারবেন । এভাবে যদি পৃথিবীর সবগুলো পিসি বা সার্ভারকে কানেক্ট করা যায় তাহলেই হয়ে যায় তাহলে আপনি পৃথিবীর সব পিসি কিম্বা সার্ভারে যা আছে তাই দেখতে পাবেন। এটাই  ইন্টারনেট। তার মানে এটা বুঝা গেলো ইন্টারনেট মানে হলো পৃথিবীর সব পিসি বা সার্ভারের কানেকশন।

মনে করুন আপনি ফেইসবুক ডটকমে ঢুকলেন! এত এত প্রোফাইল, ভিডিও, ছবি দেখতে পাচ্ছেন! এগুলোর কোনটাই আপনার পিসিতে নাই। তাহলে এগুলো কোথা থেকে আসছে? এগুলো সবই আসতেছে ফেইসবুকের ডেটা সেন্টার থেকে। তার মানে কি ব্যাপারটা এই দাঁড়ালো ফেইসবুকের ডেটা সেন্টারের সাথে আপনার পিসির কানেকশন আছে? হ্যাঁ! ঠিক ধরেছেন। আপনার পিসি ইন্টারনেটে কানেক্টেড থাকা মানে ফেইসবুকের সার্ভারের সাথেও কানেক্টেড। এখন কথা হলো পৃথিবীর সবগুলো পিসির সাথে কানেকশন কেমনে করলো? ভাভাগো ভাভা!

পৃথিবীতে যতগুলো দেশ আছে সবগুলো অপটিক্যাল ফাইবার দিয়ে কানেক্টেড। এই ক্যবলগুলো ডেটা ট্রান্সমিশন স্পিড খুবই  উচ্চমানের। ১০০ থেকে ১৫০ জিবিপিএস এর মত। এই ক্যাবলগুলো মুলত সাগরের তলদেশে বিছিয়ে দেওয়া হয়েছে। সেই ক্যাবলেরই একটা প্রান্ত প্রতিটি দেশেই আছে। এটাকে বলা হয় ল্যান্ডিং পয়েন্ট। বাংলাদেশে দুইটা ল্যান্ডিং পয়েন্ট আছে একটা হল কক্সবাজারে আরেকটা হল কুয়াকাটায়। পাশের দেশ মায়ানমারে আছে ৩টা, ইন্ডিয়ায় আছে বেশ কয়েকটা। পুরো দেশের অন্যান্য সার্ভার বা পিসি এই ল্যান্ডিং পয়েন্টের সাথে কানেক্টেড। এজন্য আমরা দেশের বা দেশের বাইরের যেকোন ওয়েবসাইট/ডেটা দেখতে পাই। সাবমেরিন ক্যাবলের ম্যাপ দেখলে ব্যাপারটা আরো পরিষ্কার হবে।

Source- https://www.submarinecablemap.com/

তো এখানে দুইটা প্রশ্ন আসতে পারে এক, ইন্টারনেট আমার ঘর পর্যন্ত কিভাবে আসে; দুই, আমরা যে ফোনে ইন্টারনেট ব্যবহার করতেছি সেখানে তো তার দিয়ে কানেক্টেড না, তাহলে কেমনে কি!

বাসাবাড়ি পর্যন্ত ইন্টারনেট সংযোগ পৌঁছানোর ক্ষেত্রে মোট ৩ টা কোম্পানি কাজ করে-
Tier 1 কোম্পানিঃ এরা সাগরে অপটিকাল ফাইভার ক্যাবল বিছিয়ে রেখেছে এবং ভিবিন্ন দেশে ল্যান্ডিং পয়েন্ট রেখেছে। যেমন, বাংলাদেশে বাংলাদেশ সাবমেরিন ক্যাবল কোম্পানি

Tier 2 কোম্পানিঃ এদের কাজ হলো ল্যান্ডিং পয়েন্ট থেকে সংযোগ নিয়ে সারাদেশে সাপ্লাই দেয় এবং নির্দিষ্ট পরিমান ডেটার জন্য নির্দিষ্ট পরিমান এমাউন্ট Tier-1 কে দেয়। যেমন, এয়ারটেল, গ্রামীনফোন, টেলিটক। এরাই সিগ্নালের মাধ্যমে ইন্টারনেট ছড়িয়ে দেয় যা আমরা মোবাইলে ব্যাবহার করি। এই কাজটা  গ্রামীন, এয়ারটেল নিজ নিজ টাওয়ারের মাধ্যমে করে থাকে।

Tier 3 কোম্পানিঃ এরা হচ্ছে ভিবিন্ন ISP কোম্পানি যারা লোকালি বা এরিয়া ভিত্তিক  ইন্টারনেট সংযোগ প্রোভাইড করে। যেমন, ধানমন্ডিতে- MazedaBD, KS Network ! সে সংযোগই অনেকে পিসিতে সরাসরি ক্যাবলের মাধ্যমে কানেকশন নেয় অনেকে বাসার রাউটারে নেয়! রাউটার ওয়াইফাই সিগ্নালের মাধ্যমে নির্দিষ্ট রেঞ্জের মধ্যে ডিভাইসগুলোতে ইন্টারনেট সংযোগ পৌঁছে দেয়।

সো, বুঝাই যাচ্ছে ইন্টারনেট ব্রাউজ মানেই হলো ডাটার দৌড়াদুড়ি। অথ্যাৎ, নির্দিষ্ট একটা ডেটা দেখার জন্য রিকুয়েস্ট করি সে ডেটা টা রিপ্লাই হিসেবে আমার কাছে চলে আসে। আমরা যখন কোন একটা ওয়েবসাইট ব্রাউজ করার চেষ্টা করি সেটা রিকুয়েস্ট হিসেবে ওই ওয়েবসাইট যেখানে হোস্ট করা আছে সেখানে রিকুয়েস্ট হিসেবে যায় তারপর রিপ্লাই হিসেবে আমাদেরকে সেই পেইজটা দেখিয়ে দেয়। ওয়েবসাইটটা যদি দেশের বাইরে কোথাও হোস্ট করা থাকে তাহলে রিকুয়েস্টটা ল্যান্ডিং পয়েন্ট হয়ে সার্ভার পর্যন্ত যত পথ অতিক্রম করে তারপর রিপ্লাই হিসেবে আমাদেরকে ওই পেইজটা দেখিয়ে দেয়।

এরকম হাজার রিকুয়েস্ট এদিক সেদিক প্রতিনিয়ত দোড়াদুড়ি করছে, অগনিত ডেটা অপটিকাল ফাইভার ক্যাবল দিয়ে এদিক সেদিক যাচ্ছে প্রতি মুহুর্তে। কিন্তু একজনের রিকুয়েস্ট অন্যজনের কাছে যায়না, কিম্বা একজনের রিপ্লাই আরেকজনের কাছে যায়না। এই ব্যাপারগুলোর জন্য কম্পিউটার সায়েন্সে নেটওয়ার্কং নামের আলাদা একটা সাবজেক্টই আছে। কারো জানার আগ্রহ থাকলে Data Communication and Networking by Forouzan এবং Computer Networking: A Top-Down Approach by Kurose and Ross পড়তে পারেন।

আমাদের একটা রিকুয়েস্ট কোন কোন দেশ হয়ে সার্ভার পর্যন্ত যায় তা আমরা নিজেরাই চেক করতে পারি অথবা আমরা চাইলেই দেখতে পারি আমাদের ব্রাউজ করা ফেইসবুক বা যেকোন ওয়েবসাইট কোন সার্ভার থেকে আসতেছে। পুরোটাই নেটওয়ার্কিং এর খেলা।

তো কথা হলো ইন্টারনেট সংযোগই যদি না থাকে ডেটা আসবে কিভাবে, রিকুয়েস্ট যাবে কিভাবে? আম্রিকায়  থাকা ফেইসবুকের ডেটা সেন্টার থেকে ফেইসবুকের পেইজ দেখাবে কিভাবে? হোপফুলি ব্যাপারগুলো এখন বুড়িগঙ্গা পানির মত অপরিষ্কার নয়।

তথ্যসূত্র-
১। https://en.wikipedia.org/wiki/Submarine_communications_cable
২। https://www.submarinecablemap.com/
৩। https://en.wikipedia.org/wiki/Internet_service_provider

গ্রাফ থিওরি - ২ঃ ভেরিয়েবলে গ্রাফ ইনপুট নেওয়া

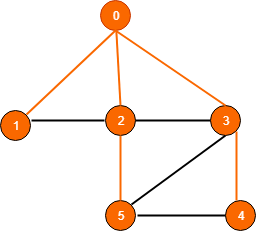
চিত্রে একটি আনওয়েটেড গ্রাফ দেখা যাচ্ছে। এই গ্রাফ নিয়ে প্রোগ্রামিং করতে হলে গ্রাফটাকে আগে ইনপুট নিতে হবে। কিন্তু প্রোগ্রামিং এ ইনপুট নিবো কিভাবে? সেখানে তো এরকম দাগ-টাগ টানা যায়না। এজও দেওয়া যায়না। তাইলে কেমনে কি :|

আসলে এখানে যে চিত্র আমরা দেখতে পাচ্ছি তা শুধুমাত্র কল্পনা, ভিজুয়ালাইজেশন বা ডেটা স্টোর করার একটা কৌশল, এছাড়া কিছু না। তাই আপাতত গ্রাফ-ট্রাফ টাইপের চিন্তাভাবনা থেকে থেকে একটু বের হয়ে যাই। ধরে নেই এটা কোন গ্রাফ না। জাস্ট একটা চিত্র। প্রতিটা বৃত্তকে এক একটা ঘর হিসেবে কল্পনা করি-

তো চিত্রে দেখে কি মনে হচ্ছে? ০ থেকে ১, ২, ৩ নাম্বার ঘরে যেতে পারি; ১ থেকে ০ এবং ২ এ যেতে পারি; ২ থেকে ১, ০, ৩, ৫ এ যেতে পারি; ৩ থেকে ০, ৫, ৪ এ সরাসরি যেতে পারি।

তো আমরা যদি ইনপুট এমনভাবে নিতে পারি যাতে এ সম্পর্কগুলো বজায় থাকে তবেই কাজ শেষ। তোমরা নিজেরা কিছুক্ষন চিন্তাভাবনা করো কোন পদ্ধতি খুঁজে পাও কিনা।

যদি কিছু খুঁজে না পাও এইদিকে আসো। উপরের সম্পর্কটাকে একটা লিস্ট আকারে সাজাই-
০-> ১, ২, ৩ //০ থেকে ১, ২, ৩ এ যাওয়া যায়
১-> ০, ২     //১ থেকে ০, ২ তে যাওয়া যায়। এভাবে সবগুলো
২-> ১, ০, ৩, ৫
৩-> ০, ৫, ৪
৪-> ৩, ৫
৫-> ২, ৩, ৪

উপরের লিস্ট টা দেখে তুমি আবার চিত্রটা ড্র করার চেষ্টা করো। যদি তুমি পেরে যাও তাহলে ধরে নাও তোমার অর্ধেক শেখা হয়ে গেছে।

তো এই কাজটা প্রোগ্রামিং এ করবো কিভাবে? তুমি চাইলে ২ডি অ্যারে ব্যাপারটা চেষ্টা করে দেখতে পারো। একটু হিন্ট দেই-

graph[0][1]  //০ থেকে ১ এ যাওয়া যায়
graph[0][2]  //০ থেকে ২ এ যাওয়া যায়
graph[0][3] //০ থেকে ৩ এ যাওয়া যায়
.
.
graph[5][2]
graph[5][3]
graph[5][4]

দেখোতো পারো কিনা! হবে কিনা আমিও শিওর না।  যদি এভাবে পেরে যাও আমাকে জানাবা। ট্রিট দিলেও দিতে পারি ;) (চোখ টিপের মানে হলো শর্ত প্রযোজ্য)

তো, তোমরা যারা জাভা পারো তারা এই কাজটাকে খুব সুন্দরভাবে করতে পারবে। ৬ টা অ্যারেলিস্ট নাও! প্রতিটা অ্যারে লিস্ট ভিতরে তার  সাথে কানেক্টেড নোডগুলোকে ঢুকিয়ে দিলেই ভেজাল শেষ।

ArrayList<Integer>[] graph = new ArrayList[6];  //৬ টা অ্যারেলিস্ট নিলাম। অ্যারেলিস্ট অব অ্যারে

graph[0] = new ArrayList<>();   //প্রথম অ্যারেলিস্ট এর যায়গা এলোকেট করলাম। জাভা জানলে এটা বুঝার কথা

graph[0].add(1);    //০ অ্যারেলিস্টের সাথে ১ কানেক্টেড
graph[0].add(2);
graph[0].add(3);

graph[1] = new ArrayList<>(); // ১ নাম্বার অ্যারেলিস্টের জন্য যায়গা এলোকেট করা
graph[1].add(0);
graph[1].add(2);

এভাবে আমরা কোন একটা অ্যারেলিস্ট দেখেই বলে দিতে পারবো তার সাথে কোন কোন নোড কানেক্টেড আছে। এখানে প্রতিটি অ্যারেলিস্ট এক একটা নোড হিসেবে কাজ করছে। উপরে গ্রাফ স্টোরের যে পদ্ধতি নিয়ে আলোচনা করলাম তার একটা নাম আছে আর তা হলো এডজেসেন্সি লিস্ট।

এই কাজটা সি প্লাস প্লাস এর ভেক্টর দিয়েও করা যায়। বলে রাখা ভালো ভেক্টর এবং অ্যারেলিস্টের কাজ একই। দুইটাই ডায়নামিক্যালি মেমরি এলোকেট করে ডেটা স্টোর করে। তোমাদের কাজ হলো পুরো গ্রাফটাকে স্টোর করা এবং একটা লুপ চালিয়ে কার সাথে কে কানেক্টেড তা প্রিন্ট করে দেখানো উপরের লিস্টের মত।

গ্রাফ স্টোর করার আরেকটা পদ্ধতি আছে তা হলো- এডজেসেন্সি ম্যাট্রিক্স। এই পদ্ধতিতে একটা ২ডি অ্যারেতে গ্রাপ ইনপুট নেওয়া হয়। গ্রাফে যতগুলো নোড আছে ২ডি অ্যারের সাইজ ঠিক ততটাই নিতে হয়। যেমন উপরের গ্রাফের ক্ষেত্রে হবে graph[6][6] !

এখন এইটার ভিতর আমাদের গ্রাফটা ঢুকাবো কেমনে? সেই পুরান কাহিনী। কইলেই বুইঝা ফেলবা

graph[0][0] = 0 //০ এর সাথে ০ এর কানেকশ নাই
graph[0][1] = 1 //০ এর সাথে ১ এর কানেকশন
graph[0][2] = 1 //০ এর সাথে ২ এর কানেকশন
graph[0][3] = 1 //০ এর সাথে ৩ এর কানেকশন
graph[0][4] = 0 //০ এর সাথে ৪ এর কানেকশন নাই
graph[0][5] = 0 //০ এর সাথে ৫ কানেকশন নাই

বুঝতেই পারতেছো কি করছি। যার সাথে যার কানেকশন আছে তার ঘরে ১ বসায়া দিচ্ছি আর যার সাথে যার কানেকশন নাই তার ঘরে বসায়া দিছি শুন্য। এভাবে বাকি নোডগুলোর ক্ষেত্রেও কিন্তু একই কেইস।

graph[1][0]--------------------graph[1][5] // ১ এর সাথে যার যার কানেকশন আছে সেই ঘরে ১ নাহলে ০
graph[2][0]--------------------graph[2][5]
.
.
graph[5][0]--------------------graph[5][5]

যারা বুঝতেছোনা কি ঘটছে তারা নীচের টেবিলটার দিকে তাকাও। নিজের প্র্যাক্টিস করার খাতার ছবিই দিয়ে দিলাম। লিখতে আলসেমি লাগতেছে। যাকগে আমার হাতের লেখার দিকে তাকালে মাইর খাবা :|

অ্যাডজেসেন্সি ম্যাট্রিক্স

এভাবে বাকিগুলো। তারপর আমরা ছোট্ট একটা লুপ চালিয়ে এদের ভিতরে ভেলু চেক করে খুব সহজেই বলে দিতে পারবো কার সাথে কার কানেকশন। তো তোমরা এই কাজটাও কইরালাও এবং লুপ চালায়া প্রিন্ট করো কার সাথে কার প্রেম বালুবাসা!

আমিও ইমপ্লিমেন্ট করছি তোমরা নিজেরা করে তারপর দেইখা নিতে পারো। আমি অ্যাডজেন্সি লিস্ট সি প্লাস প্লাস এর ভেক্টর দিয়ে করছি। তোমরা অন্য যেকোন ল্যাংগুয়েজ বা অ্যারেলিস্ট/লিংক লিস্ট হেন তেন ব্যবহার করতে পারো।

ক্ষ্যাতমার্কা কোডিং করছি এইটারে স্মার্ট করার দায়িত্ব তোমাদের। এই ধরো-
১। অ্যাডজেসেন্সি ম্যাট্রিক্স
২। অ্যাডজেন্সি লিস্ট

টাইম কমপ্লেক্সিটিঃ তো গ্রাফ স্টোরের দুইটা পদ্ধতি দেখলাম। এই দুইটার মধ্যে কোনটা ভালা? তুমি যেহেতু এই পোস্টটা পড়তেছো আমি ধরে নিচ্ছি তুমি টাইম কমপ্লেক্সিটির/মেমরি কমপ্লেক্সিটির কিচ্ছাকাহিনী গেবনে একবার হলেও শুনছো।

অ্যাডজেন্সি ম্যাট্রিক্স এর কথাই আগে কই। একটা গ্রাফে যতগুলো এজ থাকুকনা কেন ডেটা রাখার জন্য তোমাকে n*n সাইজের অ্যারে ডিক্লেয়ার করা লাগবে। উপরের গ্রাফে মোট এজ আছে ৯টা কিন্তু আমরা ইউজ করছি মোট 6*6 = 36 টা ইন্টেজার। মানে এডজেন্সি ম্যাট্রিক্স এর মেমরি কমপ্লেক্সিটি n^2। তবে অ্যাডজেন্সি ম্যাট্রিক্স এর একটা সুবিধা হলো কোন নোডের সাথে কোন নোড কানেক্টেড তা আমরা O(1) কমপ্লেক্সিটিতেই পেয়ে যাবো। যদি বলি ০ এর সাথে ৩ এর কানেকশন আছে কিনা আমরা সিমপ্লি graph[0][3] চেক করলেই বুঝে যাবো। তবে বড় সাইজের কোন গ্রাফের ক্ষেত্রে অ্যাডজেন্সি লিস্ট ইউজ না করাই ভালো। এতে হিতে বিপরীত হতে পারে।


এইবার আসি অ্যাডজেন্সি লিস্টের কথা। অ্যাডজেন্সি ম্যাট্রিক্স এর সমস্যা বুঝতে পারছো সে কেন বেশী মেমরি খায়? আমরা সেখানে কানেক্টেড এবং নন কানেক্টেড সবগুলো নোডেরই ট্র্যাক রাখতেছি। কিন্তু কেন ভাই? যার অস্তিত্বই নাই তার ট্র্যাক রাখার কেন দরকার। অ্যাডজেসেন্সি লিস্ট ঠিক এই কাজটাই করছে। তার সাথে যার কানেকশন শুধু তারে তার দলে রাখছে। এভাবে সবগুলো নোডই এই কাজটা করছে। এতে মেমরি কনজাম্পশন কমে আসছে। এটার মেমরি কমপ্লেক্সিটি কত এবং আর একটা নোডের কানেক্টেড সব নোড খুঁজে বের করতে কি পরিমান সময় লাগবে? এইটা খুঁজে বের করা তোমার কাজ।  আজ এই পর্যন্তই! টা  টু

ডিফেন্ডেন্সি সমাচারঃ ম্যাভেন/গ্র্যাডল জিনিসগুলো কি? খায় না মাথায় দেয়?

বিল্ড ইন লাইব্রেরি নিয়ে ত্যানা পেঁচানোঃ তোমরা নিশ্চয়ই সি দিয়ে স্ট্রিং এর ভিবিন্ন অপারেশন করেছো। স্ট্রিং কম্পেয়ার করা, স্ট্রিং এর লেন্থ বের করা, একটা স্ট্রিং এর মধ্যে কয়টা ওয়ার্ড আছে তা কাউন্ট করা মনে আছে? আবার দুইটা নাম্বারের মধ্যে কোনটা ছোট কোনটা বড়, দুইটা ভেরিয়েবলের মধ্যে সোয়াপ করা, স্কয়ার রুট বের করা! এসব কাজ কিন্তু তোমার সি প্রোগ্রামিং ভিতর অলরেডি করা আছে।  যেখানে এই জিনিসগুলো করা থাকে সেগুলোকে বলা হয় লাইব্রেরি। যেমন, স্ট্রিং সমস্ত অপারেশনের জন্য <string> নামের একটা লাইব্রেরি আছে, ম্যাথের সমস্ত অপারেশন করার জন্য <math.h> নামক একটা লাইব্রেরি আছে। এসব লাইব্রেরির ভিতরে অসংখ্য ফাংশন লেখা আছে আমরা সেই ফাংশনগুলোকে দিয়ে কাজ করানোর জন্য সেই ফাংশনগুলোর নাম ধরে কল করলেই পেয়ে যাবো। তার আগে যেটা করতে হয় তা হলো সেই লাইব্রেরি আগে আমার প্রজেক্টে ইঙ্কলুড করে নিতে হবে। যেমন, স্ট্রিং এর জন্য #include <string>, ম্যাথের জন্য #include <math.h> এরকম অসংখ্য লাইব্রেরি আছে সি প্রোগ্রামিং ল্যাঙ্গুয়েজে। যা দিয়ে আমরা অনেক কাজ দ্রুত শেষ করে ফেলতে পারি। দুইটা নাম্বারকে সোয়াপ করার জন্য swap(number1, number2), স্কয়ার রুট বের করার জন্য sqrt(number), স্ট্রিং এর লেন্থ বের করার জন্য strlength(myString[]) এরকম আরো অনেক।

নতুন যারা ডেভেলপমেন্ট শুরু করে বিশেষ করে এন্ড্রয়েড বা জাভা রিলেটেড কোন প্রজেক্টে কাজ করে তাদের প্রথমেই একটা যায়গায় হোঁচট খেতে হয়। সেটা হলো ম্যাভেন/গ্রাডল। এই জিনিসগুলোর উপর নবীনরা এতটাই বিরক্ত যে এটার নাম শুনলেই তারা ভয় পায়। আসলে ব্যপারটা ভয় পাওয়ার কিছু না। আমাদের কাজগুলোকে সহজ করার জন্যই এদের উৎপত্তি। যাইহোক মুল কথায় আসি।

মনে করো, তুমি একটা এন্ড্রয়েড অ্যাপ বানাবা যেখানে ম্যাপ থাকবে। এখানে ম্যাপে মুলত তোমার যে কাজটা বের করতে হবে তা হলো নিয়ারবাই লোকেশন বের করা, এক যায়গায় থেকে অন্য যায়গার দুরত্ব বের করা এরকম অনেক ধরনের ম্যাপ রিলেটেড অপারেশন। কিন্তু তার জন্য তো ম্যাপের দরকার হবে। এক্ষেত্রে তোমার হাতে দুইটা অপশন এক, তোমাকে ম্যাপ তৈরী করা আর দুই, অলরেডী তৈরী করা ম্যাপটা নিয়ে আসা। যেহেতু অলরেডি সেটা তৈরী করা আছে সেটা আবার তৈরী করার কোন মানে নাই। এজন্য যা লাগবে তা হলো ম্যাপের লাইব্রেরিটা প্রজেক্টে নিয়ে আসা। এজন্য তোমাকে যেটা করতে হবে তা হলো ম্যাপের লাইব্রেরিটা  ডাউনলোড করে তা প্রজেক্টে যুক্ত করা। এখানে অনেক ঝামেলা পোহাতে হবে তোমাকে। প্রথমত, প্রজেক্টের কোন ফোল্ডারে রাখবা সেটা নিয়ে কনফিউশন, দ্বিতীয়ত, কোন রকমে যদি ভার্সন পরিবর্তিত হয় তাহলে এই লাইব্রেরি রিমুভ করে  নতুন ভার্সন যুক্ত করা যা অতিরিক্ত ঝামেলা। এমন যদি হতো কেউ একজনকে জাস্ট কমান্ড দিয়ে দিবো সে নিজ থেকেই এসব কিছু ম্যানেজ করে নিবে। ব্যাপারটা আরো সুন্দর হয়না? তোমাকে বাড়তি কোন ঝামেলায় পড়তে হচ্ছেনা। এই কাজটাই আসলে করে ম্যাভেন বা গ্রাডল। এদের প্রত্যেকেরই আলাদা আলাদা স্ট্রাকচার আছে। গ্র্যাডলের ক্ষেত্রে ব্যপারটা এরকম-

 dependencies {  
   compile 'com.google.maps.android:android-maps-utils:0.5+'  
 }  

এই জিনিসটাই গ্র্যাডল ফাইলে লিখলে ম্যাপের জন্য যা যা লাইব্রেরি প্রয়োজন তা সে ডাউনলোড করে নিবে। আর ভার্সন চেঞ্জ হলে ভার্সনের নাম্বার বলে দিলেই  কাজ শেষ। সে তার মত করে ডাউনলোড করে নিবে। এরকম ভিবিন্ন ফ্রেমওয়ার্কের জন্য ভিবিন্ন ডিফেন্ডেন্সি ম্যানেজমেন্ট সিস্টেম আছে। যেমন, স্প্রিং এর জন্য ম্যাভেন।

আশাকরি ম্যাভেন/গ্র্যাডল নিয়ে কনফিউশনগুলো ক্লিয়ার হয়ে গেছে।

সি পয়েন্টার - ১ঃ ছ্যাঁচড়া তত্ব

আলম এবং সেফাত পরস্পর বন্ধু। সেফাতের একটা অভ্যাস হলো আলমের পিছনে গোয়েন্দাগিরি করা। আই মিন, আলম কোথায় যায় কি করে সেই খবর সে রাখে, আরো ছ্যাঁচড়াভাবে বললে পিছে পিছে ঘুরে আর কি। আলম এতে মাইন্ড করেনা কারন সেফাতকে আলম অনেক বিশ্বাস করে নিজের গফের চেয়েও বেশী। তো, তুমি যদি জিজ্ঞেস করো আলম এখন কোথায়? গুলিস্তান, ধোলাইখাল যেখানেই থাকুক না কেন সে হুবহু বলে দিতে পারবে তাইনা?  আর তোমাকে বিশ্বাস করানোর জন্য সে আলমকে সাথে নিয়ে সেলফিও তুলে দিতে পারবে। ব্যপারটাই স্বাভাবিক।

মনে করো আলমকে আমি ১০ টাকা দিলাম এবং সেফাতকে আলমের পেছনে লাগায়া দিলাম। সেফাত যেহেতু আলমকে ফলো করে আলমকে দিয়ে আমি সে টাকাটা ফিরিয়ে আনতে পারবো তাইনা? একইভাবে সেফাতকে দিয়ে আমি আলমের কাছে টাকাটা পাঠিয়েও দিতে পারবো।

এখানে আলম একটা ভেরিয়েবল হিসেবে কাজ করছে আর ছ্যাঁচড়া সেফাত পয়েন্টার হিসেবে কাজ করছে। পয়েন্টারের কাজই হলো কোন একটা ভেরিয়েবলকে পয়েন্ট করা/অ্যাড্রেস রাখা/ফলো করা একই কথা।  কোন একটা পয়েন্টার যখন কোন একটা ভেরিয়েবলের অ্যাড্রেস রাখে তখন ওই পয়েন্টার সেই ভেরিয়েবলের সমস্ত ইনফরমেশন জানতে পারে।

পয়েন্টার সি প্রোগ্রামিং এর গুরুত্বপূর্ণ এবং শক্তিশালী একটা জিনিস যা সরাসরি মেমরির সাথে জড়িত। এটা দিয়ে অনেক কাজ খুব দ্রুত সময়ে কমপ্লিট করা যায়।

আমরা জানি ভেরিয়েবলের কাজ হলো ডাটা রাখা, যেমন আলম ১০ টাকা রাখছে। পয়েন্টারের কাজ হলো সেই ভেরিয়েবলের অ্যাড্রেস রাখা। কাউকে ফলো করা আর তার অ্যাড্রেস জেনে রাখা একই জিনিস। অনেকে প্রশ্ন করতে পারো ভেরিয়েবলের অ্যাড্রেসটা আবার কি, তাদের জন্য-

আমরা সবাই জানি, ভেরিয়েবল ডিক্লেয়ার করলে সে মেমরিতে একটা যায়গা তৈরী করে নেয় এবং ডাটাটা সেখানে রেখে দেয়।  প্রতিটা যায়গারই একটা অ্যাড্রেস থাকে। পয়েন্টার সেই অ্যাড্রেসটাই জমা রাখে। একটা ভেরিয়েবলের সামনে & বসালেই তার অ্যাড্রেস পাওয়া যায়। নীচের প্রোগ্রামে দেখো আলমের কাছ থেকে কিভাবে তার অ্যাড্রেস জানতেছি

 #include <stdio.h>  
 int main()  
 {  
   int alom = 10; //alom k 10 taka diye dilam B-)  
   printf("Total taka in alom: %d\n", alom);    //alom er kache koto taka ache ta jantechi
   printf("Address of Alom: %d\n", &alom);  //alom ekhon koi ache ta jantechi 
   return 0;  
 }  

 OUTPUT  
 Total taka in alom: 10  
 Address of alom: 6356748  

এখন যে কাজটা করবো তা হল সেফাতকে আলমের পিছনে লাগায়া দিবো। আই মিন, সেফাতকে বলবো আলমের পিছে পিছে ঘুরতে। সেফাতের কাজই হলো যেহেতু আলমের অ্যাড্রেস জেনে রাখা তাই সেফাতের আগে অবশ্যই * দিতে হবে। ছ্যাঁচড়াদের আইডেন্টিফাই করার জন্য তার আগে স্টেরিক ব্যবহার করতে হয়।

 #include <stdio.h>  
 int main()  
 {  
   int alom; //alom aslo 
   alom= 10; //alom re 10 taka dilam 
   int *sefat; //chesra sefat re hajir korlam 
   sefat = &alom; //sefat re alom er address chinaya disi. lou thela 
   printf("alom er kache taka ache: %d\n", alom);    //printing the value of alom
   printf("sefat er kache alom er address: %d\n", sefat); //seeing the address of alom from sefat
   return 0;  
 }  

 OUTPUT  
 alom er kache taka ache: 10  
 sefat er kache alom er address: 6356748  

এখন আমরা চাইলে সেফাতের কাছ থেকে জানতে পারবো আলমের কাছে কত টাকা আছে-

 #include <stdio.h>  
 int main()  
 {  
   int alom = 10;  
   int *sefat;  
   sefat = &alom;  
   printf("%d", *sefat); //Sefat is showing the value in alom   
   return 0;  
 }  

 OUTPUT   
 10  

আবার যদি চাই আলমের কাছের যে টাকা আছে তা পরিবর্তন করতে সেটা কিন্তু আমরা সেফাতকে দিয়েই করতে পারবো। মনে করো আমি সেফাতকে বললাম আলমের কাছে এখন ২০ রাখো। সেফাত দ্রুত আলমের কাছে গিয়ে ২০ টাকা রেখে দিবো।

 #include <stdio.h>  
 int main()  
 {  
   int alom = 10;  
   int *sefat;  
   sefat = &alom;  
   *sefat = 20;  //Changing the value of alom by sefat 
   printf("Current value of alom: %d", alom); //Printing the value of Alom   
   return 0;  
 }  

 OUTPUT   
 10  

দেখতে পাচ্ছো আমরা কিন্তু আলমকে কিছুই বলিনাই। সেফাতরে দিয়ে ঘটনা ঘটিয়ে ফেললাম। অথ্যাৎ, সেফাতকে দিয়ে আলমের ভেলু পরিবর্তন করে ফেললাম। চাইলে কিন্তু আলমের ব্যালান্স শুন্যও করে দিতে পারি। সো, বি কেয়ারফুল।

সেফাত এবং আলমের মধ্যে কিন্তু একটা জিনিসের মিল আছে। তারা কেউ ই একসাথে একাধিক ভেলু রাখতে পারেনা। আলম যেমন একসাথে একাধিক ভেলু রাখতে পারেনা আবার সেফাত একসাথে একাধিক লোককে ফলো করতে পারেনা। সেফাত ডিজিটাল ছ্যাঁচড়া। একসাথে একাধিক মানুষের সাথে চামচামি সে একদমই পছন্দ করেনা। তো, কোনভাবে সেফাতকে যদি কেকা নামের একজন ব্যাক্তির অ্যাড্রেস ধরায়া দিতে পারি তাহলে কিন্তু সে আর আলমকে ফলো না করে কেকাকে ফলো করবে।

  #include <stdio.h>  
  int main()  
  {  
   int alom = 10;  
   int keka = 999;  
   int *sefat;  
   sefat = &alom; // sefat ekhon alom k follow kortese  
   printf("Sefat er point kora address a j value pawa gelo: %d\n", *sefat);  //alomer value
   sefat = &keka; // Sefat ekhon kekappike follow kortese  
   printf("Sefat er point kora jaygay bortoman value: %d\n", *sefat);  //kepapir value
   return 0;  
  }  

 OUTPUT  
 Sefat er point kora address a j value pawa gelo: 10  
 Sefat er point kora jaygay bortoman value: 999  

সেফাত বড্ড বেড়ে গেছে। যাকে তাকে ফলো করে বসতেছে। তুমি চাইলে কিন্তু সেফাতকে পুরা ডাম্ব করে দিতে পারো। মানে সে কাউকেই ফলো করবেনা। এটা করতে হলে সেফাতকে একটা NULL দিয়ে দাও। ভেজাল শেষ। বিশ্বাস না হলে করে দেখো, সে তোমাকে কোন ভালু বা অ্যাড্রেস কিছুই দিতে পারবেনা।

তুমি কি জানো একটা অ্যারের নাম নিজেই একটা পয়েন্টার? অথ্যাৎ, আমাদের যদি একটা অ্যারে হয় int myArr[] = {50, 60, 70, 80, 90} এখানে myArr হলো একটা পয়েন্টার যার কাছে থাকবে প্রথমজনের অ্যাড্রস।  মানে হলো myArr এর কাছে থাকে myArr[0] এর অ্যাড্রেস। বিশ্বাস না হলে *myArr প্রিন্ট করে দেখো তোমার আউটপুট আসবে 50.

  #include <stdio.h>  
  int main()  
  {  
    int myArr[] = {50, 60, 70, 80, 90};  
    printf("%d", *myArr);  
   return 0;  
  }  

 OUTPUT   
 50  

এখন সেই অ্যাড্রেসটা যদি সেফাতকে দেখিয়ে দিতে পারি তাহলে কিন্তু সে এবার কেকাকে ভূলে গিয়ে এখানে এসে myArr[0] কে পয়েন্ট করবে। বুঝতেই পারছো সেফাত এখন কোন ভালুটা আউটপুট দিবে।

 #include <stdio.h>  
 int main()  
 {  
   int myArr[] = {50, 60, 70, 80, 90};  
   int *sefat = myArr;  
   printf("%d", *sefat);  
   return 0;  
 }  

 OUTPUT   
 50  

অ্যারেতে মেমরি ব্লক হিসেবে কাজ করে অথ্যাৎ, সবগুলো ভেরিয়েবল পাশাপাশি যায়গা করে নেয় সেহেতু পয়েন্টারকে এক এক করে বাড়িয়ে আমরা সবগুলো ভেলু এক্সেস করতে পারি। যেমন, সেফাতকে এক বাড়ালে সে পরের অ্যাড্রেসে যাবে, তখন সে ভেলু দিবে আবার এক বাড়ালে তার পরে যাবে এবং তখন সে ভেলু দিবে ৭০। এভাবে আমরা শেষ পর্যন্ত লুপ চালিয়ে কাজটা করতে পারি। নিজে নিজে চেষ্টা করে দেখো। এই ব্যাপারে বিস্তারিত জানতে পারবে এখানে ! আজ এই পর্যন্তই।
টা টা!

অব্জেক্ট অরিয়েন্টেড প্রোগ্রামিং - ১২ঃ অ্যানোনিমাস ইনার ক্লাস

অ্যানোনিমাস ইনার ক্লাস হলো এক ধরনের ক্লাস যার কোন নাম নাই। এই কথা শুনে অনেকে হয়তো টাস্কি খেয়ে গেছো; নামবিহীন আবার ক্লাস হয় নাকি! একটু পরেই ব্যপারটা আরো ক্লিয়ার হবে। নীচের প্রোগ্রামটা খেয়াল করো। আমি একটা PersonalData নামের একটা ইন্টারফেস তৈরী করলাম এবং সেটাকে ইমপ্লিমেন্ট করার জন্য MyClass নামের আরেকটা ক্লাস তৈরী করলাম এবং কাজটি সম্পর্ন করলাম।

Program - 1: 

 public interface PersonalData {  
      int x = 20;   
      public void getAge();   
 }  

 public class MyClass implements PersonalData {  
      @Override  
      public void getAge() {  
           System.out.println("The age is: "+ x);  
      }  
 }  

 public class MainClass {  
      public static void main(String[] args) {  
           MyClass myClass = new MyClass();  
           myClass.getAge();  
      }  
 }  

 OUTPUT  
 20  

মেইন মেথড থেকে কল করে আমি সিমপ্লি getAge() মেথডটি ব্যবহার করতে পারবো, যার আউটপুট হবে ২০। পুরো কাজটা অক্ষত রেখে কোনভাবে যদি MyClass ক্লাসটিকে হাওয়া করে দিতে পারি তখনই Anonymous Inner ক্লাসের ব্যপারটা চলে আসে। আমরা কাজটা করেই ফেলি!

Program - 2:

 public interface PersonalData {  
      int x = 20;   
      public void getAge();   
 }  

 public class MainClass {  
      public static void main(String[] args) {  
           /* Creating the object of the interface implementing the   
            overloading method */  
           PersonalData personalData = new PersonalData() {  
                @Override  
                public void getAge() {  
                     System.out.println("The age is: "+ x);  
                }  
           };  
           personalData.getAge();  
      }  
 }  

 OUTPUT  
 20  

কোন পার্থক্য খুঁজে পেয়েছো? এখানে কিন্তু MyClass নামের ক্লাসটি নাই। কিন্তু আমাদের আউটপুট ঠিকই আছে। এখানে আমরা ইন্টারফেসটি ইমপ্লিমেন্ট করার জন্য আলাদা ক্লাস ইউজ না করে সরাসরি ইন্টারফেসটির অব্জেক্ট তৈরী করেছি এবং তার আনইমপ্লিমেন্টেড মেথডগুলো ইমপ্লিমেন্ট করে দিয়েছি একইসাথে। এর ফলে আমরা মাঝখানের ক্লাসটিকে এভয়েড করে ফেলছি। এখানে MyClass ই Anynomous ক্লাস হিসেবে কাজ করছে আর যেহেতু এটি MainClass নামক অন্য একটি ক্লাসের ভিতর কাজ করছে তাই একে Anynomous Inner ক্লাস বলা হয়। তাহলে আমরা অ্যানোনিমাস ইনার ক্লাসের একটা সংজ্ঞায় উপনীত হতে পারি-

অ্যানোনিমাস ইনার ক্লাস হল এমন এক ধরনের ক্লাস যেটা কোন ইন্টারফেস বা অ্যাবস্ট্র্যাক্ট ক্লাসের সাবক্লাস তৈরী করা ছাড়াই অব্জেক্ট তৈরী করতে সহায়তা করে।